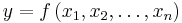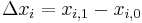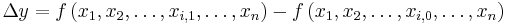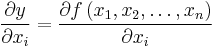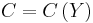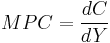Marginal value
A marginal value is
- a value that holds true given particular constraints,
- the change in a value associated with a specific change in some independent variable, whether it be of that variable or of a dependent variable, or
- [when underlying values are quantified] the ratio of the change of a dependent variable to that of the independent variable.
(This third case is actual a special case of the second).
In the case of differentiability, at the limit, a marginal change is a mathematical differential, or the corresponding mathematical derivative.
These uses of the term “marginal” are especially common in economics, and result from conceptualizing constraints as borders or as margins.[1] The sorts of marginal values most common to economic analysis are those associated with unit changes of resources and, in mainstream economics, those associated with instantaneous changes. Marginal values associated with units are considered because many decisions are made by unit, and marginalism explains unit price in terms of such marginal values. Mainstream economics uses instantaneous values in much of its analysis for reasons of mathematical tractability.
Contents |
Quantified conception
Assume a functional relationship
Discrete change
If the value of  is discretely changed from
is discretely changed from 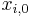 to
to 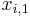 while other independent variables remain unchanged, then the marginal value of the change in
while other independent variables remain unchanged, then the marginal value of the change in  is
is
and the “marginal value” of  may refer to
may refer to
or to
Example
If an individual saw her income increase from $50000 to $55000 per annum, and part of her response was to increase yearly purchases of amontillado from 2 casks to three casks, then
- the marginal increase in her income was $5000
- the marginal effect on her purchase of amontillado was an increase of 1 cask, or of 1 cask per $5000.
Instantaneous margins
If instantaneous values are considered, then a marginal value of  would be
would be 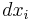 , and the “marginal value” of
, and the “marginal value” of  would typically refer to
would typically refer to
(For a linear functional relationship 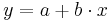 , the marginal value of
, the marginal value of  will simply be the co-efficient of
will simply be the co-efficient of  (in this case,
(in this case,  ) and this will not change as
) and this will not change as  changes. However, in the case where the functional relationship is non-linear, say
changes. However, in the case where the functional relationship is non-linear, say 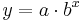 , the marginal value of
, the marginal value of  will be different for different values of
will be different for different values of  .)
.)
Example
Assume that, in some economy, aggregate consumption is well-approximated by
where
 is aggregate income.
is aggregate income.
Then the marginal propensity to consume is